Parallel Scrambler Generator
Scramblers are used in many communicaton protocols such as PCI Express, SAS/SATA, USB, Bluetooth to randomize the transmitted data. To keep this post short and focused I’ll not discuss the theory behind scramblers. For more information about scramblers see [1], or do some googling. The topic of this post is the parallel implementation of a scrambler generator. Protocol specifications define scrambling algorithm using either hex or polynimial notation. This is not always suitable for efficient hardware or software implementation. Please read my post on parallel CRC Generator about that.
The Parallel Scrambler Generator method that I’m going to describe has a lot in common with the Parallel CRC Generator. The difference is that CRC generator outputs CRC value, whereas Scrambler generator produces scrambled data. But the internal working of both based on the same principle.
Here is an example of a scrambler with the polynomial G(x) = x16+x5+x4+x3+1
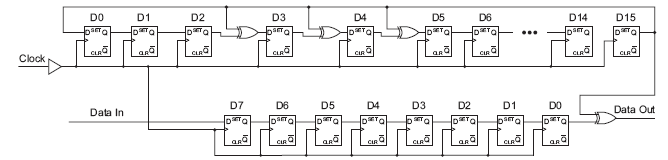
Following is the description of the Parallel Scrambler Generator algorithm:
(1) Let’s denote N=data width, M=generator polynomial width. 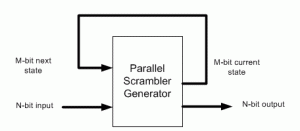
(2) Implement serial scrambler generator using given polynomial or hex notation. It’s easy to do in any programming language or script: C, Java, Perl, Verilog, etc.
(3) Parallel Scrambler implementation is a function of N-bit data input as well as M-bit current state of the polynomial, as shown in the above figure. We’re going to build three matrices:
- Mout (next state polynomial) as a function of Min(current state polynomial) when N=0 and
- Nout as a function of Nin when Min=0.
- Nout as a function of Min when Nin=0
Note that the polynomial next state doesn’t depend on the scrambled data, therefore we need only three matrices.
(4) Using the routine from (3) calculate scrambled data for the Mout values given Min, when Nin=0. Each Min value is one-hot encoded, that is there is only one bit set.
(5) Build MxM matrix, Each row contains the results from (4) in increasing order. For example, 1’st row contains the result of input=0×1, 2′nd row is input=0×2, etc. The output is M-bit wide, which the polynomial width.
(6) Calculate the Nout values given Nin, when Min=0. Each Nin value is one-hot encoded, that is there is only one bit set.
(7) Build NxN matrix, Each row contains the results from (6) in increasing order. The output is N-bit wide, which the data width.
(8) Calculate the Nout values given Min, when Nin=0. Each Min value is one-hot encoded, that is there is only one bit set.
(9) Build MxN matrix, Each row contains the results from (7) in increasing order. The output is N-bit wide, which the data width.
(10) Now, build an equation for each Nout[i] bit: all Nin[j] and Min[k] set bits in column [i] from three matrices participate in the equation. The participating inputs are XORed together.
Nout is the parallel scrambled data.
Keep me posted if the Parallel Scrambler Generation tool works for you, or you need more clarifications on the algorithm.
References:
What a cool site, thank you for your good job! But, because English is not my home language, I have to pay more time on understanding the Parallel Scrambler Generator algorithm in this article. I think if you add an simple demo [as N = 4, M = 4 and a simple generator polynomial] of these step, people could understand this algorithm better, thank you.
@PT
Thanks for the positive feedback. I’ll add a simple example.
Very nice site and useful information and generators.
For me, it only miss one thing to be excelent: the option of generating VHDL inspite of Verilog.
Thank’s for the tools
Chico
@Chico
Hi Chico,
Thanks for the positive feedback. I’ve added VHDL support.
I have produced the scrambler for polynomial mentioned in 802.3-2005_section4(10Gbps PCS layer) for 64-bit datapath i.e. datawidth=64 and polynomialwidth=58 using the polynomial 1+x^39+x^58. The polynomial has been picked from the IEEE standard mentioned above.
The results of the scrambler are not as expected, also the equations in Verilog looked strange and there is no shifting of the scrambled register.
Dear Ahmed,
I did the following experiment. I generated two scramblers:
(1) data width=64,poly width=58, G(x)= 1+x39+x58 (1 and x^39 boxes checked)
(2) data width=1,poly width=58, G(x)= 1+x39+x58 (1 and x^39 boxes checked).
This is a serial scrambled that should produce the same output after 64 clocks as (1) given the same input.
I simulated both with different inputs and haven’t found any problems – the results always matched.
Let me know if you still experience problems,
OutputLogic
Evgeni,
Yeh that’s true but the equations regarding XOR’s does not conform to the Algorithm described in the paper below which is followed in most of the implementations.
Parallel Scrambler for High-Speed Applications
Chih-Hsien Lin, Chih-Ning Chen, You-Jiun Wang, Ju-Yuan Hsiao, and Shyh-Jye Jou
Could you provide the descriptions of the equations of Verilog HDL.
Regards,
Ahmed
Ahmed,
Thanks for the pointer.
I don’t claim that my method of generating parallel scrambler is the most efficient one in terms of speed or logic utilization. But I’ll read the paper and do the comparison.
Parallel scrambler generator is using the same approach as the parallel CRC. It’s described here: http://outputlogic.com/my-stuff/parallel_crc_generator_whitepaper.pdf
I’d need to answer another question: since a given scrambler is described by a system of linear equations, how come there are multiple solutions to it (that is, multiple ways to generate the same parallel scrambler).
hello,
excellent site, useful information and Scrambler generator
how descrambler?
did you make a generator descrambler ?
regards
jean
Jean, thanks for the comment.
Typically, scrambler and descrambler implementation is the same. That is, if you have a scrambled data input, on the output of the scrambler/descrambler you’d get the original data.
Why is that so ? To put it simple, because there is a property of two XOR operations (scrambler then descrambler) cancelling each other: I^S^S = I.
Evgeni,
Thanks for the description of parallel scrambler generator.
I have also compared your generated scrambler with that of xilinx 10G PCS reference design scrambler and the results are not matching.You can also see xapp775 and compare.
Regards,
Ahmed
Ahmed,
I looked at the scramble.v file in xapp775. The scrambler implemented there is different from what my tool generates.
Let me explain why.
line 95: assign `TPDA Scr_wire[6] = TXD_input[6]^Scrambler_Register[32]^Scrambler_Register[51];
line 226: Scrambler_Register[57] <= `TPDB Scr_wire[6]; line 221: TXD_Scr[65:0] <= `TPDB {Scr_wire[63:0], Sync_header[1:0]};
That is, the next state of the scrambler LFSR is the function of the current state of the scrambler LFSR and the input data.
What my tool generates is that the next state of the scrambler LFSR is the function of only the current state.
Both approaches use the same polynomial (G=1 +x^39 +x^58), but the results are different.
Unfortunately, different protocols use different scrambler approaches given the same polynomial.
Even in 802.3-2005_section4 spec WIS scrambler in section 50.3.3 has scrambler LFSR independent of the input data, whereas 66/64 bit scrambler in section 49.2.6 has scrambler LFSR dependent of the input data.
This is an important difference and I'll need to provide an option to generate scrambler code either way.
Evgeni,
Thanks for the analysis.
What I understand is, your scrambler generator is generating the code for “frame-synchronous scrambler” while there is another type of scrambler which is called “self synchronous scrmabler”. i.e. in 802.3-2005_section4, 50.3.3 refers to the frame-synchronous scrambler while 49.2.6 to self synchronous scrambler.
Regards,
Ahmed.
Evgeni,
Thanks for the description of parallel scrambler generator.
Your scrambler generator is generating the code for “frame-synchronous scrambler” while there is another type of scrambler which is called “self synchronous scrambler”.
Did you provide an option to generate scrambler code either way ?
And to generate descrambler code for “self synchronous descrambler” ?
Regards,
Jacques.
Evgeni,
Thanks for the description of parallel scrambler generator.
Your scrambler generator is generating the code for “frame-synchronous scrambler” while there is another type of scrambler which is called “self synchronous scrambler”.
Did you provide an option to generate scrambler code either way ?
And to generate descrambler code for “self synchronous descrambler” ?
Regards,
Jacques.
Hi Jacques,
Not yet. I was asked exact same question by a couple of other users. I’ll provide that option sometime later.
Thanks,
Evgeni
@Evgeni
How to generate a parallel unscramber ?
You had said that their implementation are same on above reply, Does it mean two circuit are identical ?
If I don’t understand, let me know how to make it.
Regards,
otkim
Hi otkim,
Yes, descrambler circuit is typically the same as the scrambler.
Thanks,
Evgeni
I am implementing a SDI interface in FPGA.
Now I am trying to make a frame synchronizer(word framing circuit).
In SD-SDI i/f, the frame sync. pattern is a 30-bit word{0x3ff, 0x000, 0x000} on unscrambed data. so a SDI receiver have to find the sequence after descrambler.
For the same purpose, is it possible to find the scrambled sequence of the sync. pattern before descrambler
Regards,
otkim
Hi otkim,
Can you point me to the SD-SDI specification – I’ll take a look.
Thanks,
Evgeni
good job!!Many thanks!!you give me more time in my job!!
I can see that it been a while since anyone have replyed or posted on this site.
So is it still monitored? and is it still possible to ask question. I have on in regard to the scrambler generator.
But i wont start explaning my problem, since it will take time, and it whould be a waste if noone will answer it anyway
Regards Vinther.
Hi Vinther,
I’ll try to answer your question.
Thanks,
Evgeni
ok .. this is a nice site and alot of help to people like me who cant just sit down and calculate this out right. However, i need a 64 bit wide x^7+x^6+1 scrambler, and i tryed your generator. however it dosnt work.
So i tryed your generator with a 1 bit wide bus to see if i could make heads and tail in how it does ..
Your generator makes this for a x^7+x^+1 scrambler with 1 bit wide bus.
”
lfsr_c(0) <= lfsr_q(6);
lfsr_c(1) <= lfsr_q(0);
lfsr_c(2) <= lfsr_q(1);
lfsr_c(3) <= lfsr_q(2);
lfsr_c(4) <= lfsr_q(3);
lfsr_c(5) <= lfsr_q(4);
lfsr_c(6) <= lfsr_q(5) xor lfsr_q(6);
data_c(0) <= data_in(0) xor lfsr_q(6);
"
But what i need it to generate is this ( also represented in 1 bit wide bus)
"
lfsr_c(0) <= lfsr_q(5) xor lfsr_q(6);
lfsr_c(1) <= lfsr_q(0);
lfsr_c(2) <= lfsr_q(1);
lfsr_c(3) <= lfsr_q(2);
lfsr_c(4) <= lfsr_q(3);
lfsr_c(5) <= lfsr_q(4);
lfsr_c(6) <= lfsr_q(5);
data_c(0) <= data_in(0) xor lfsr_q(6);
"
And according to wiki this must then be a x^-7+x^-6+1 if you look under the Additive (synchronous) scramblers section.
But i cant get your generator to generate this, is this something you can help me with. And do you know what the diffrence between the two types is. I know the above one works because ive implemented it already however it runs 64 times slower that what i need.
Thanks in advanced
/vinther
Hi Vinther,
I’m generating scrambler LFSR in Galois notation, which is more popular. You’re asking to generate it in Fibonacci notation. There is a conversion procedure of feedback taps between the two to produce equivalent implementation. Please try G(x) = x^7+x^1+1.
Wiki entry on LFSRs has some information about this.
Thanks,
Evgeni
@Evgeni
Thank you, i can see that however i have to starte with another init value in this case “1111110”, as to get the right result. Now i just have to see if that works with a 64 bit wide bus. Else i have to use my backup plan an keep all the values in memory and xor det with data.
Thanks you for you help
/Vinther
Well it worked.
Thanks alot for you help
Why don’t you use variables and generate statement… It will be easier to read and very few lines…
Hi Ashok,
There are several ways to generate the code. I just picked this one as the most “basic”. As for the generate statements, it’s specific to Verilog-2001, and many developers are still using ’95.
I guess having different options for the code generation will be a nice feature.
Also, using generate will result in less efficient code, at least for FPGA tools. I discuss it a bit in my Circuit Cellar article
Thanks,
Evgeni
Hi Evgeni,
at your generated code “data_out <= scram_en ? data_c : data_out;"
why I think it should be "data_out <= scram_en ? data_c : data_in;"
in your code if scram_en == 0, then data_out <= data_out;
this code can never work, data_out will be always the reset value…
thank you
@Jordy
I’m sorry for my mistake, 🙂
you are right, it means hold the value for next scram_en valid.
thank you
Hi Evgeni,
Thanks for a very nice tool for generating scramblers.
Are you planning to add option to generate ‘self synchronous scrambler’?
Hi,
At some point I will add the ’self synchronous scrambler’, since there are quite a few requests from the users.
Thanks,
Evgeni
Hi Evgeni,
Thanks for a nice tool and providing us deep insight about working of parallel scrambler. It was of great help. Thanks you once again.
Hi,
Do you provide stand-alone application for scrambler?
Hi,
At this moment I don’t provide a stand-alone application for the parallel scrambler generator. Can you tell why you need it, and what cannot be done with the online version ?
Thanks,
Evgeni
hi,
im confused with the signal ‘scram_rst’,can u plz explain the need of that signal? is it similar to data valid signal?
Hi,
scram_rst enables initialization of lfsr_q register with all-1’s. scram_rst is not essential; the same initialization can be done with the ‘rst’ signal.
Thanks,
Evgeni
Hi,
Thank you for your tool, very usefull
as i used to do parallel scrambler by “hand”.
Have you been looking for the self synchronous scrambler ?
any idea of modifications needed ?
thanks a lot .
Hi,
Several users have asked for a self-synchronous scrambler. I think my current approach will still work, but it’ll require quite a few modifications.
Thanks,
Evgeni
Thank you
Hi,
in scrambler, my datawidth is 64 and my polynomial width is 58, my polynomial is 1+x^39+x^58. scrambler i got. but still litle confusion in descrambler. please explain me how descrambler works as same data width, that is 64 bits.
Hi Naveen,
In most cases, descrambler code is identical to scrambler. It’s usually described in a protocol specification, unless you implement something custom.
Thanks,
Evgeni
Hi,
I used the PCIe scrambler from your website and I am trying to instantiate it in the altera FPGA. I am not sure at what point am I supposed to enable the scrambler?
At this point, I am looking at PCIe x1 lane, the deserializer is bringing out 8 bit output for this one lane. At this point the deserializer data is scrambled but 8b10b decoded. You the scram_en, scram_rst and rst signal. Ihave tied them to pcie reset signal. Is it OK to use PCIe reset signal to enable the scrambler? In this application, I am trying to de-scrambled the 8 bit scrambled data from the deserializer. I am assuming that same scrambled module can be used to de-scramble.
wire [7:0] descrambled_data;
scrambler ds1(
.data_in(rxdata0_ext[7:0]),
.scram_en(pcie_rstn),
.scram_rst(~pcie_rstn),
.data_out(descrambled_data[7:0]),
.rst(~pcie_rstn),
.clk(pclk_in)
);
Hi,
Reset input is used to initialize scrambler LFSR to all-ones.
Enable is used to qualify the data (data valid).
If your data is valid in every clock cycle, then it should work.
Thanks,
Evgeni
Hi Evgeni,
Nice tool. Has there been any progress on adding the ability to generate a self synchronous scrambler for Ethernet applications?
Thanks,
— Matt
Hi,I want descramble the USB 3.0,Can I use it’s scramble code?
Hi,
Yes, descrambler in USB 3.0 is the same as scrambling. It’s stated on page 451 in Appendix B.1 of the spec.
Thanks,
Evgeni
I used VHDL decrambling the USB 3.0’s scramble,the code was generated by Scrambler Generator Tool.the Data Width=16 of the scramble code,but I need a the Data Width=32 of the descramble code,is it OK?
Hi,
That should work. That’s the whole purpose of this tool – to generate scrambler/descrambler code with any data width.
Thanks,
Evgeni