Parallel Scrambler Generator
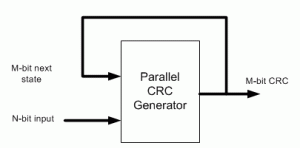
Scramblers are used in many communicaton protocols such as PCI Express, SAS/SATA, USB, Bluetooth to randomize the transmitted data. To keep this post short and focused I’ll not discuss the theory behind scramblers. For more information about scramblers see [1], or do some googling. The topic of this post is the parallel implementation of a scrambler generator. Protocol specifications define scrambling algorithm using either hex or polynimial notation. This is not always suitable for efficient hardware or software implementation. Please read my post on parallel CRC Generator about that.
The Parallel Scrambler Generator method that I’m going to describe has a lot in common with the Parallel CRC Generator. The difference is that CRC generator outputs CRC value, whereas Scrambler generator produces scrambled data. But the internal working of both based on the same principle.
Here is an example of a scrambler with the polynomial G(x) = x16+x5+x4+x3+1
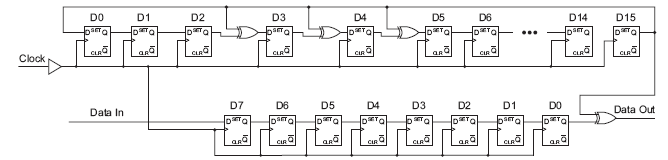
Following is the description of the Parallel Scrambler Generator algorithm:
(1) Let’s denote N=data width, M=generator polynomial width. 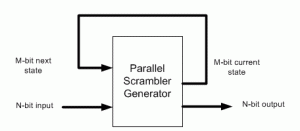
(2) Implement serial scrambler generator using given polynomial or hex notation. It’s easy to do in any programming language or script: C, Java, Perl, Verilog, etc.
(3) Parallel Scrambler implementation is a function of N-bit data input as well as M-bit current state of the polynomial, as shown in the above figure. We’re going to build three matrices:
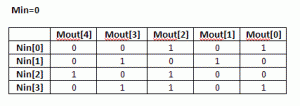
- Mout (next state polynomial) as a function of Min(current state polynomial) when N=0 and
- Nout as a function of Nin when Min=0.
- Nout as a function of Min when Nin=0
Note that the polynomial next state doesn’t depend on the scrambled data, therefore we need only three matrices.
(4) Using the routine from (3) calculate scrambled data for the Mout values given Min, when Nin=0. Each Min value is one-hot encoded, that is there is only one bit set.
(5) Build MxM matrix, Each row contains the results from (4) in increasing order. For example, 1’st row contains the result of input=0×1, 2′nd row is input=0×2, etc. The output is M-bit wide, which the polynomial width.
(6) Calculate the Nout values given Nin, when Min=0. Each Nin value is one-hot encoded, that is there is only one bit set.
(7) Build NxN matrix, Each row contains the results from (6) in increasing order. The output is N-bit wide, which the data width.
(8) Calculate the Nout values given Min, when Nin=0. Each Min value is one-hot encoded, that is there is only one bit set.
(9) Build MxN matrix, Each row contains the results from (7) in increasing order. The output is N-bit wide, which the data width.
(10) Now, build an equation for each Nout[i] bit: all Nin[j] and Min[k] set bits in column [i] from three matrices participate in the equation. The participating inputs are XORed together.
Nout is the parallel scrambled data.
Keep me posted if the Parallel Scrambler Generation tool works for you, or you need more clarifications on the algorithm.
References:
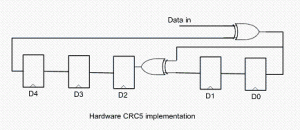
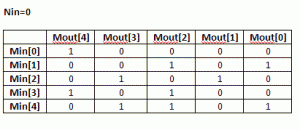 (9) Now, build an equation for each Mout[i] bit: all Nin[j] and Min[k] bits in column [i] participate in the equation. The participating inputs are XORed together.
(9) Now, build an equation for each Mout[i] bit: all Nin[j] and Min[k] bits in column [i] participate in the equation. The participating inputs are XORed together.